on Euclid's Elements.aux
LECTURES ON EUCLID'S ELEMENTS - Book I

LECTURES ON EUCLID'S ELEMENTS - Book I

Eric Lehman and Martti Pesonen

revised Feb 21, 2008

Contents

on Euclid's Elements.toc
LECTURES ON EUCLID'S ELEMENTS Book I
This compact introduction to the dynamic geometry-algebra computer program GeoGebra is created especially for the needs of a short course on Euclid's Elements Book I, taught in February-March 2008 at the University of Joensuu by professor Eric Lehman (University of Caen, France) during his Erasmus teacher exchange visit.
GeoGebra is a free open source code computer program which can be invoked online (through internet: GeoGebra WebStart) or installed on a computer and used offline.
The created dynamic figures can be Exported to a Dynamic Worksheet on a Web page.
The URL address of GeoGebra main Web page is http://www.geogebra.org/

1  Fundamental plane geometry objects

1.1  Basic objects - exercises with GeoGebra

The basic objects in geometry are points, segments, lines, rays, circles, angles, triangles, quadrangles, parallelograms etc.
Start GeoGebra and use the View menu to "uncheck" (hide) all "checked" choices (chosen to be visible). Then you should only see a rectangular part of a plane without any signs of coordinate systems (which still exist behind, but do not have to be used explicitly).
Change the language to be English (Options etc).
Example 1 a) Create two points called A and B. If the point labels (names) are not seen, make them visible (right-click the point and use the appearing menu).
b) Construct a segment a between these points and a point C on this segment. Change the colour of C to red.
Drag the segment around on the screen; use its endpoints and the segment itself.
c) Construct a line through some other points D and E.
What happens when you place C and D on top of each other, what happens when you separate them again?
d) Drag the segment so that it intersects with the line. Create the point of intersection; call it I. Try to drag I. What happens?
e) Create a ray starting from C and passing through D.
f) In the menu View click on Algebra Window. Change the color of the last ray to green by clicking on the name of that ray in the Algebra Window.
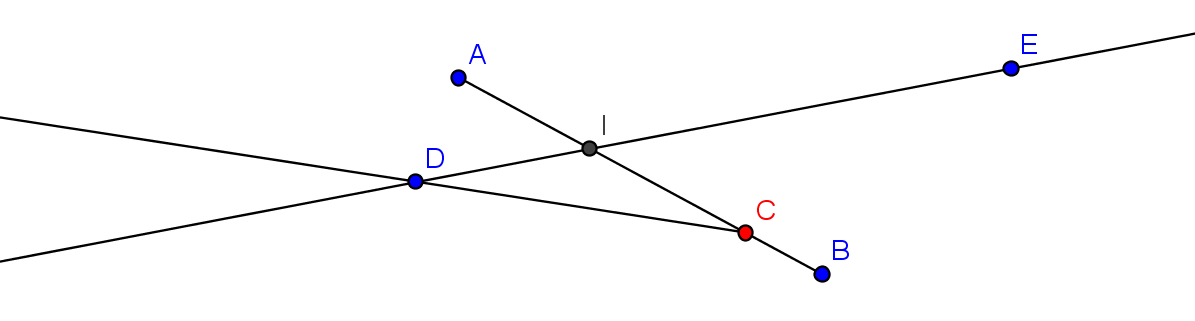Figures/1PointSegmentLineRay.png
Figure 1: Point, segment, line, ray
Example 2 a) Create two points called O and P. If the point labels (names) are not seen, make them visible (right-click the point and use the appearing menu).
Construct a circle called c with center O and the point P on this circle.
Drag the circle around on the screen. Move the center, move P.
b) Construct a segment AB and a circle d with center A through the point B.
Move this circle so that it intersect c at two different points I and J.
c) What happens when you separate the circles; look at the Algeba Window (menu View etc)?
d) You may ask GeoGebra about relations between the objects in a figure; the format is:
Relation[object1, object2].
Ask GeoGebra the following questions (use the Input field, see View menu):
Relation[c,I]: answer 
Relation[c,d]: answer 
Figures/2Circles.png
Figure 2: Circles and intersections
Exercise 3 a) Create an equilateral triangle with a given side AB. You choose first the two vertex points A and B.
Hint. Start with creating two circles with centers at the two points and going through the other point ...
b) How can you construct isosceles triangles?
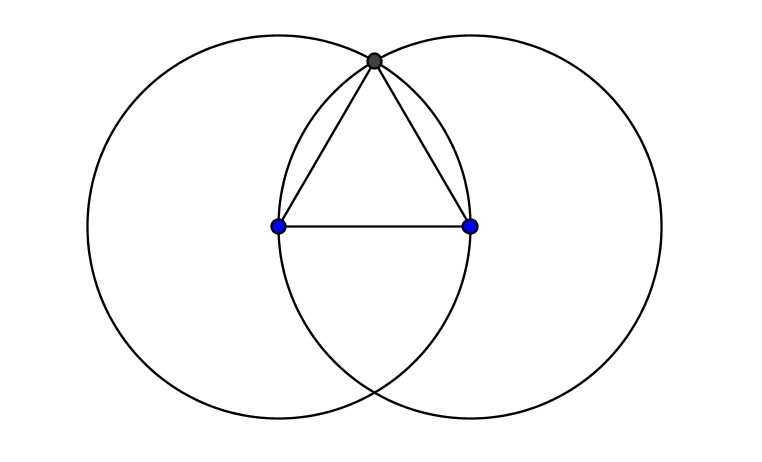Figures/3EquilateralTriangle.png
Figure 3: Equilateral triangle with a given side
Exercise 4 Take away axes, grid etc.
Do the Desargues' Theorem construction as follows:
1. Create a point S.
2. Create a triangle ABC.
3. Draw the rays starting from S through A, B and C; call them p, q and r, respectively.
4. Take a point A¢ on p, B¢ on q and C¢ on r.
5. Create the triangle A¢B¢C¢.
6. Create the lines BC and B¢C¢ and their intersection point P.
7. Create the lines CA and C¢A¢ and their intersection point Q.
8. Create the lines AB and A¢B¢ and their intersection point R.
9. Draw the line QR, call it s.
10. Ask GeoGebra the question Relation[P,s].
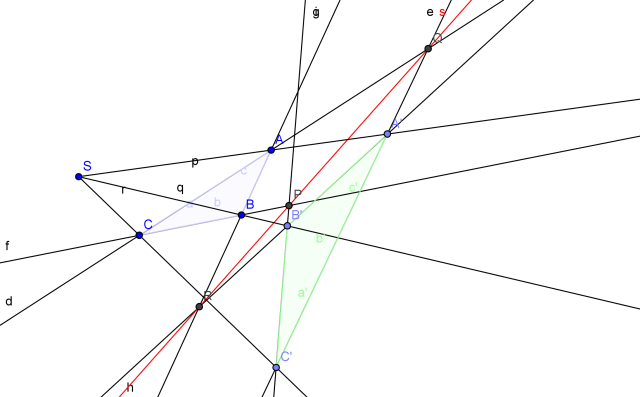Figures/DesarguesDirect.png
Figure 4: Desargues' configuration
Question. Two triangles ABC and A¢B¢C¢ are centrally perspective if AA¢, BB¢ and CC¢ are convergent. They are axially perspective if the points P, Q and R are collinear (where P, Q and R were defined above in 6, 7 and 8).
Express in these terms the Desargues' Theorem. What is the converse?
Exercise 5 Verification of the converse of Desargues' theorem.
1. Choose two points P and Q.
2. Draw the line s through P and Q.
3. Choose a point R on s.
4. Choose any point A.
5. Draw the line c through A and R.
6. Choose a point B on c.
7. Draw the line a through B and P and the line b through A and Q.
8. Let us call C the intersection of a and b.
9. Choose any point A¢.
10. Draw the line c¢ through A¢ and R¢.
11. Choose a point B¢ on c¢.
12. Draw the line a¢ through B¢ and P¢ and the line b¢ through A¢ and Q¢.
13. Let us call C¢ the intersection of a¢ and b¢.
14. Draw the line p through A and A¢.
15. Draw the line q through B and B¢.
16. Draw the line r through C and C¢.
17. Call S the intersection of p and q.
18. Ask the question Relation[S,r].
19. Conclude.
Exercise 6
Let ABC be a triangle and let H be the orthocenter of the triangle ABC (that is: H is the intersection of the line through A orthogonal to BC and the line through B orthogonal to CA, and in fact H is then also on the line through C orthogonal to AB). Draw the circumcircles to the triangles HBC, HCA and HAB.
What can you guess about these three circles?
Check your conjecture with the computer.
Prove your theorem!

File translated from TEX by TTH, version 3.33.
On 21 Feb 2008, 20:22.